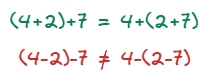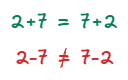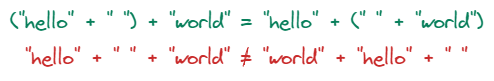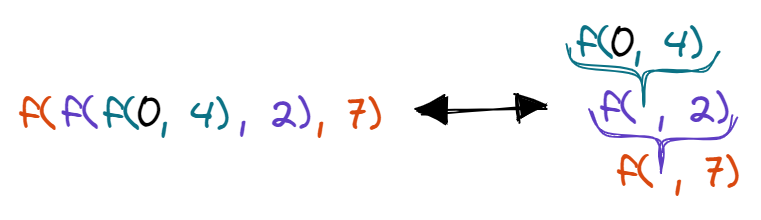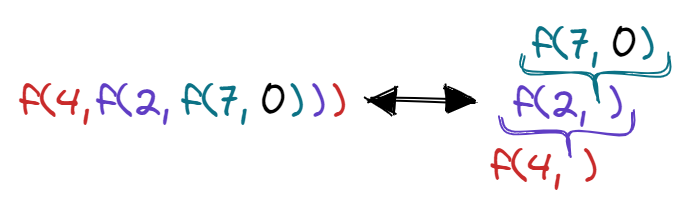Understanding Scala folds

One of the first things that you encounter in the functional programming world are functions that operate on collections. In this post, I will focus on the fold operation. It might sometimes be as confusing as it is common in our programs, especially when used with non-associative or non-commutative operators. Don’t worry if you don’t know what it means, more on that below!

This post was inspired by my deep dive into Haskell after reading Learn You a Haskell for Great Good! book. I highly recommend reading it!

Some explanation first

What is a fold?

Instead of a direct definition or quoting the documentation, I would like to describe it in the simplest way possible. The fold is an operation that takes an init element and a collection and then aggregates (folds) it into a single value. This single value can be anything - a sum, a concatenation, or even a new collection. Simple, isn’t it?

What are associativity and commutativity?

When an operation is associative, it means that no matter how we put parentheses in it, the result will be the same. For example, addition is associative, whereas subtraction is not.

Commutativity property means that the order of operands does not matter in the operation. We can observe it again on addition, which is commutative, and on subtraction, which is not.

Quite often these properties come together, but that’s not always the case. For instance, string concatenation is associative but not commutative.

Why are we talking about this? Because both of these properties matter for folds. You’ll see how our results may be affected by that in the next sections.

Types of folds

Three methods allow folding in Scala: foldLeft, foldRight, and fold. The first two have associativity (or if you prefer - direction) specified in their names, and the third one is a fold that doesn’t have a predefined order of operations. fold defaults to foldLeft and can be overridden if the collection supports a more efficient way of unordered folding. It won’t be covered in this post in detail.

foldLeft

Let’s take a look at the most common of the folds, foldLeft. According to the documentation:

Applies a binary operator to a start value and all elements of this collection, going left to right.

In my opinion, it’s better to think about this operation as a fold that associates to the left. Why? Because it doesn’t really go from left to right, let me explain.

Assume that we have a List(4, 2, 7), an init value of 0, and a binary operation f. In the code it can be described as:

List(4, 2, 7).foldLeft(0)(f)

foldLeft will construct the following expression:

We start with an initial value of 0. Then f is applied on 0 and 4. Then, f is applied to the result of the previous operation, and 2. The same thing happens for 7. Did we go from left to right? Kind of, we went through the list from left to right to construct a whole expression which then was evaluated as the final result. The result is a consequence of parentheses in the expression rather than the direction itself.

The important thing to note is that the final result of foldLeft is f of the accumulated value and the last element of the list. I’ll refer to that fact later.

Implementation

We can implement foldLeft for a List[A] using tail recursion:

@tailrec
final def foldLeft[B](z: B)(f: (B, A) => B): B =
  list match {
    case head :: tail => tail.foldLeft(f(z, head))(f)
    case Nil          => z
  }

This means that foldLeft is stack-safe, and you won’t see StackOverflowErrors. Note that the evaluation terminates on the very last element so the whole list is always traversed.

Examples

Let’s assume that f is addition:

List(4, 2, 7).foldLeft(0)((acc, int) => acc + int) // 13

Note that the accumulator in foldLeft is on the left. This means that we can simplify the above to:

List(4, 2, 7).foldLeft(0)(_ + _) // 13

What would happen though if we defined it like this?

List(4, 2, 7).foldLeft(0)((acc, int) => int + acc) // 13

Well, nothing. The result will be the same because addition is commutative.

Okay, that’s boring. We just went from left to right and applied added both operands in both cases. Let’s take a look at another f, subtraction this time.

List(4, 2, 7).foldLeft(0)(_ - _) // -13

We received the same number but with a minus, seems reasonable. Now, we’ll swap the operands again:

List(4, 2, 7).foldLeft(0)((acc, int) => int - acc) // 9

And we get 9. 9? Why 9? Weren’t we just applying subtraction from left to right in this case too?

Well, we were but the f in this case swapped the order of operands. This means that f affects the result of non-commutative operations, like subtraction or string concatenation. Even when we know that we cannot freely swap the operands here, it’s hard to predict the result without analyzing the expression tree. There we have it, our first caveat of folds!

foldRight

You might have guessed that foldRight associates the operations to the right. Using the same List(4, 2, 7), we’ll jump straight into the expression formed by:

List(4, 2, 7).foldRight(0)(f)

It gives us:

Note that the initial 0 is now on the right side of the list. If you understood how foldLeft works, it should be easy to understand foldRight. But this is where the fun begins!

Implementation

The most straightforward implementation of foldRight for List[A] is via recursion:

def foldRight[B](z: B)(f: (A, B) => B): B =
  list match {
    case head :: tail => f(head, tail.foldRight(z)(f))
    case Nil => z
  }

We have to begin the evaluation from the last element of the list, so we build a chain of recursive calls until we reach the end. This has a major disadvantage though. We’ll sooner or later run out of stack frames because of stack overflows.

We can definitely do better. If we have to start from the end of the list, why don’t we just put the last element at the beginning by reversing the list? This is a thing that we can do in a stack-safe way. How? Via foldLeft!

def reverse: List[A] =
  list.foldLeft(List.empty[A])((acc, a) => a :: acc)

Here, we are using fold to transform one collection into another one. So now, how can we perform a foldRight on a reversed list? Again, via foldLeft. Surprising, isn’t it?

def foldRight[B](z: B)(f: (A, B) => B): B =
  list.reverse.foldLeft(z)((acc, a) => f(a, acc))

We have a stack-safe implementation of foldRight, but it comes at a cost. By using foldLeft twice, we are also traversing the list twice. This is a thing to consider when we want to use foldRight.

Scala standard library implements foldRight exactly this way.

Examples

If you understand foldLeft, understanding the examples for foldRight should be easy.

// Equivalent of:
//   List(4, 2, 7).foldLeft(0)(_ + _)
// as addition is associative and commutative.
List(4, 2, 7).foldRight(0)(_ + _) // 13

// Equivalent of:
//   List(4, 2, 7).foldLeft(0)(_ - _)
List(4, 2, 7).foldRight(0)((int, acc) => acc - int) // -13

// Equivalent of:
//   List(4, 2, 7).foldLeft(0)((acc, int) => int - acc)
List(4, 2, 7).foldRight(0)(_ - _) // 9

Note that by convention, the accumulator for foldRight is the right argument of f. This is a thing that may help you or confuse you more, especially when using wildcards.

The last interesting example of foldRight use case is appending to a list. If we are starting the evaluation from the end, we can add a single element or a whole list to the end effortlessly:

List(4, 2, 7).foldRight(List(0))(_ :: _) // List(4, 2, 7, 0)

To infinity, and beyond!

Do you remember that the final result of foldLeft is f of the accumulated value and the last element of the list? For foldRight, it is f of the first element and the accumulated value. Why might it be useful?

Imagine that we have quite a long list of booleans… perhaps an infinite one.

We now may want to apply the logic and to that whole list and get a result. We definitely have an intuition that no matter what is in the infinity, the fold should return false because the second element of the list is false. Note that and is not strict in its second argument. That means that if we have false && someValue, someValue won’t be evaluated because the result can be returned just by evaluating the first argument.

Let’s try to define this list in the code and fold it via foldLeft:

val infiniteBooleans = true #:: false #:: LazyList.continually(true)
infiniteBooleans.foldLeft(true)(_ && _)

We’ve put true here as the init element as it is a neutral element of the logical and. The result of the above program is not something that we want though, it just hangs. The reason for this is the fact that foldLeft has to evaluate the last element to return the result, as mentioned above. Because the list is infinite, it’ll never reach that element. Non-strictness of and doesn’t help here at all.

Luckily, we have foldRight! It just needs the first element for the final result so if we supply a non-strict f, it should work even for infinite lists. As and is associative and commutative, we can just change foldLeft to foldRight and we are done:

infiniteBooleans.foldRight(true)(_ && _)

Now we receive the result imme… wait, it still hangs. Why? It turns out that foldRight for LazyLists still uses that trick with reverse and foldLeft that was mentioned above. This means that we are still limited by the foldLeft constraints. Luckily, we can fix that ourselves:

extension [A](lazyList: LazyList[A]) {
  def lazyFoldRight[B](z: B)(f: (A, => B) => B): B =
    lazyList match {
      case head #:: tail => f(head, tail.lazyFoldRight(z)(f))
      case _ => z
    }
}

lazyFoldRight recursively calls itself to evaluate the final value. f has type (A, => B) => B which means that the second argument won’t be evaluated if it is not needed. Unfortunately, we cannot make use of tail recursion here. This method will suffer from stack overflows if the result requires evaluating too many elements. However, it allows us to use it like:

infiniteBooleans.lazyFoldRight(true)(_ && _)

and get false immediately. Awesome!

Summary

In this post, we went through the implementation details and fun facts about folds. I hope that you know now how they differ from each other, how to use them, and what kind of unexpected behaviors you may encounter. What is more, the knowledge that you’ve gained also applies to reduce, as it can be implemented via fold.

You may be wondering now whether foldLeft or foldRight is better. The answer is quite straightforward. If your operation is associative, then use foldLeft. If it isn’t, just use the fold that calculates the correct result. In rare cases of infinite lists and non-strict f, you have to implement your own lazyFoldRight which will terminate quickly enough to not overflow the stack.

Thank you for reading!