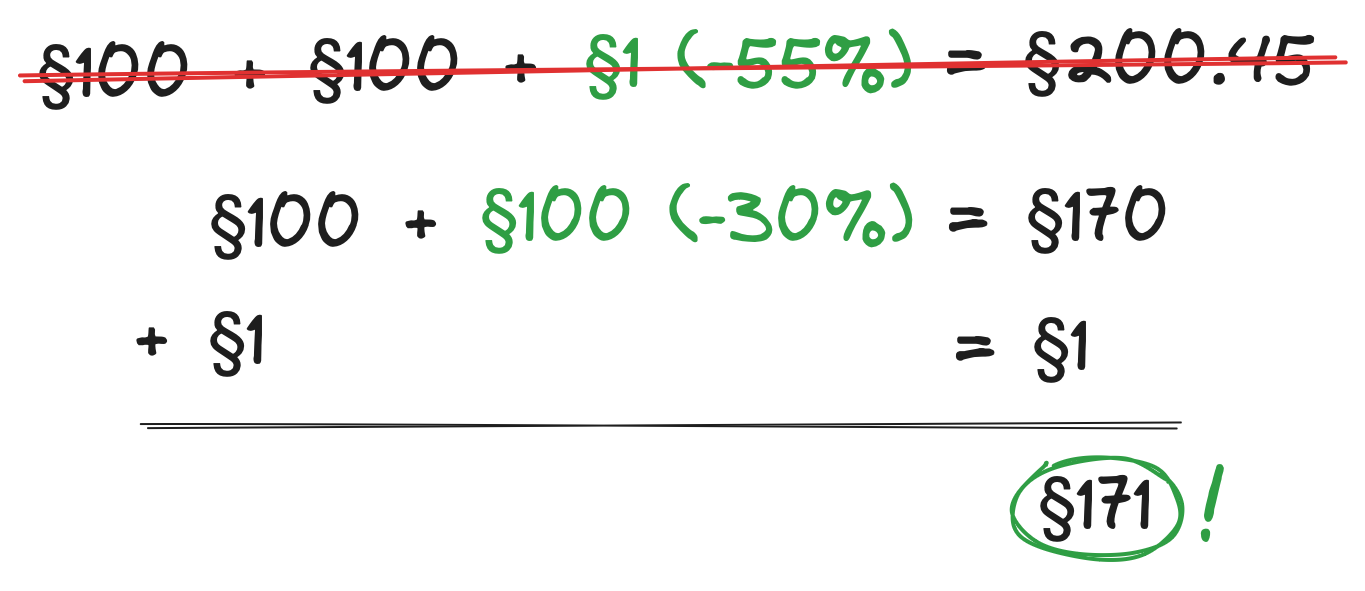Cleo algorithm: How I saved money using Scala

We often perceive programming as a way to earn money a hobby, yet seldom consider its potential for saving money. In this post, I share a story of how I reduced some expenses through the implementation of a simple algorithm in Scala.

Background

In Poland, there is a store specializing in home appliances with a rather unconventional discount program. At first glance, the program appears straightforward: the more products you purchase, the greater the discount you receive. For the sake of this discussion, let’s abstract from the Polish currency and utilize Simoleons.

Here’s how the discount program works:

Products in the cart	Discount
1	None
2	-30% off the cheapest product
3	-55% off the cheapest product
4	-80% off the cheapest product
5 or more	The cheapest product for §1

You might already see an opportunity for cost optimization here. Consider this scenario: you wish to purchase three products priced at §100, §100, and §1. If bought together, the total cost is §200.45. However, by splitting the purchase into two orders - (§100, §100) and (§1) - you’d only pay §171! This strategy seems like a reasonable way to save some money, doesn’t it?

This observation inspired me to devise a dedicated algorithm to tackle this problem: the Cleo algorithm.

The algorithm’s name is a nod to the name of the artist featured in the store’s advertisements 😄

The algorithm

I have to be honest - I didn’t delve into any purely mathematical methods to solve the problem. Instead, I opted to brute force the optimal split. Along the way, I’ll explain a few simplifications I made. While there’s certainly room for improvement, I rarely find myself purchasing such a large number of products that would necessitate further optimization. Let’s walk through the steps.

Types

First, let’s define some types to aid our reasoning about the entities we’ll manipulate.

type Price = Double
case class Product(name: String, price: Price)
type ProductGroup = Set[Product]
type ProductGroupCombination = Set[ProductGroup]

Here, ProductGroup represents a subset of items you wish to order, and ProductGroupCombination is a collection of product groups that collectively contain all the items you want to order. The meanings of Price and Product are self-explanatory.

Here, you’ll notice the first simplification: you cannot have two products with the same name and price. There are various ways to address this, such as assigning different names to identical products or introducing an additional field to Product, like seqNo: Int = 0, to distinguish between each occurrence.

Finding the cheapest combination

Let’s begin by defining our desired outcome and then delve into the details. Our primary objective is to identify a ProductGroupCombination with the smallest total price.

The process unfolds as follows:

1. Determine all possible ProductGroupCombinations for the given ProductGroup.
2. Calculate the price for each combination, factoring in the discount.
3. Identify the combination with the lowest total price.

This process can be easily translated into Scala code:

def findCheapestCombination(products: ProductGroup): (ProductGroupCombination, Price) =
  getProductGroupCombinations(products) // 1
    .map { combination => // 2
      val totalPrice = combination.map(calculatePriceWithDiscount).sum
      combination -> totalPrice
    }
    .minBy { case (_, totalPrice) => totalPrice } // 3

Calculating the price with discount

Determining the price of a ProductGroup with discounts is a straightforward process. Here’s what we need to do:

1. Sort the products by price in ascending order.
2. Apply the discount to the cheapest product based on the discount table outlined in the Background section.
3. Sum the price of the cheapest product with the prices of all other products.

Let’s see how this translates into Scala code:

def calculatePriceWithDiscount(products: ProductGroup): Price = {
  def calculateDiscountPrice(cheapestPrice: Price) = // 2
    products.size match {
      case 0 | 1 => cheapestPrice
      case 2 => cheapestPrice * (1 - 0.3)
      case 3 => cheapestPrice * (1 - 0.55)
      case 4 => cheapestPrice * (1 - 0.8)
      case _ => 1
    }

  products.toList.sortBy(_.price) match { // 1
    case cheapest :: rest =>
      calculateDiscountPrice(cheapest.price) + rest.map(_.price).sum // 3
    case Nil => 0
  }
}

Note the simplicity of the code, facilitated by Scala’s built-in pattern matching, sortBy, and sum functions!

Finding all product group combinations

This is the most intricate aspect of the problem, yet it’s surprisingly straightforward, thanks to the methods available on a Set. While there are likely multiple approaches to achieving this, here’s the method I’ve devised:

1. If the ProductGroup is empty, return a Set with a single, empty ProductGroupCombination.
2. Otherwise, identify all non-empty subsets of the input product group. For instance, if the input is {plushie, snack, crayon}, the subsets would include {plushie, snack, crayon} (yes, the same as the input), {plushie, snack}, {snack, crayon}, {plushie, crayon}, {plushie}, {snack}, and {crayon}. Here, Scala’s subsets method is particularly helpful.
3. For each subset, determine all combinations of the remaining products. For example, if the subset is {plushie}, the remaining product combinations would be [{snack, crayon}] and [{snack}, {crayon}].
4. Merge each combination with the corresponding subset, generating a ProductGroupCombination. The final result is a Set[ProductGroupCombination].

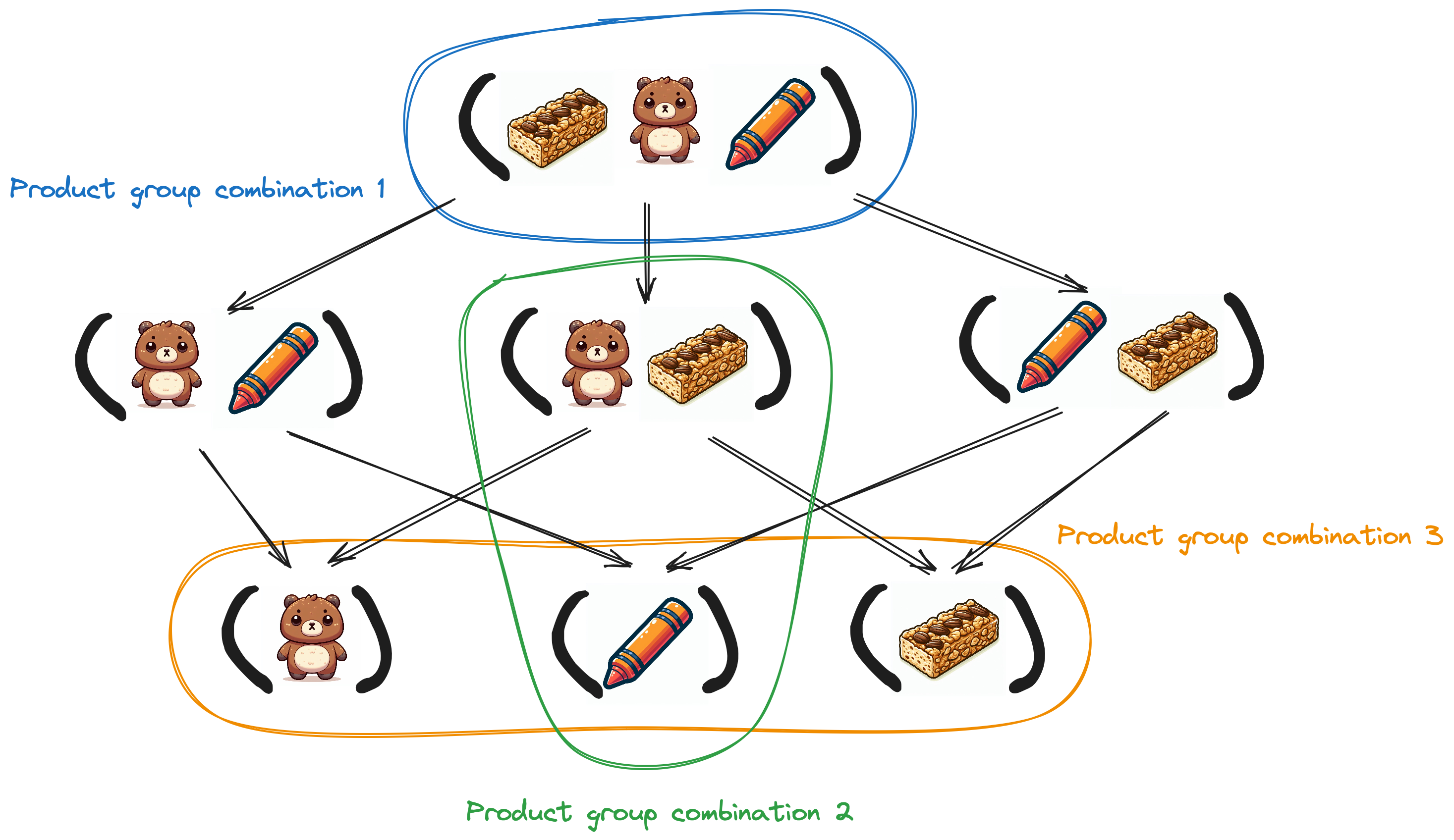Example subsets and product group combinations

Here’s the corresponding Scala code:

def getProductGroupCombinations(products: ProductGroup): Set[ProductGroupCombination] =
  if (products.isEmpty) // 1
    Set(Set.empty)
  else {
    for {
      subset <- products.subsets.filter(_.nonEmpty) // 2
      otherSubsets <- getProductGroupCombinations(products.diff(subset)) // 3
    } yield otherSubsets + subset // 4
  }.toSet

The use of toSet at the end deduplicates a potentially lengthy list of found combinations. Additionally, it’s worth noting that the recursive call to getProductGroupCombinations is NOT tail-recursive, which may result in a stack overflow for larger inputs. It’s worth considering optimization in this area if necessary.

Putting it all together

With all the utilities outlined above, we can now optimize our order effortlessly. Calculating the cheapest combination is now as simple as making a function call:

val products = Set(
  Product("plushie", 2699),
  Product("glowstick", 1599),
  Product("crayon", 1699),
  Product("bubblewrap", 1299),
  Product("snack", 2599)
)
val (cheapestCombination, lowestPrice) = findCheapestCombination(products)

// Single order price is 8597.0
// The cheapest order combination is [{bubblewrap, crayon, glowstick}, {plushie, snack}] with price 8400.85

In the above scenario, we saved almost §200! It was certainly worth the effort.

Summary

In this post, we went through a real-life use case of messing around with a store discount program for our own benefit cost optimization using Scala. Of course, the algorithm could be written in any language but thanks to many Scala features, it is concise and simple. I hope you’re now inspired to look for minor things around you that can be automated and optimized via a few lines of code.

Full code is available on Scastie: https://scastie.scala-lang.org/HkbDPS8dQqKplIrcpJrvAQ